Qué es una función lineal: ejemplos

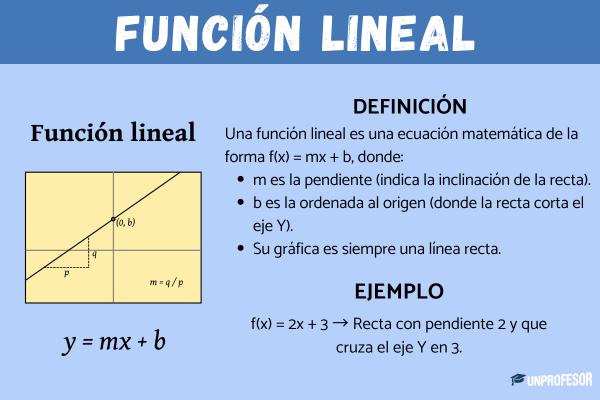
Una función lineal es una relación matemática entre dos variables. Es una función polinómica de grado uno que tiene la siguiente forma:

F(x) = mx + b

Donde m es la pendiente de la función, b es la ordenada al origen y x es la incógnita.

También puede escribirse como:

y = mx + b

Y la gráfica de una función lineal siempre es una línea recta en el eje cartesiano.

Ejemplos de funciones lineales son:

• y= 3x + 5
• y = -2x -1
• y = x - 3
• y = -4x + 8
• y = 5x

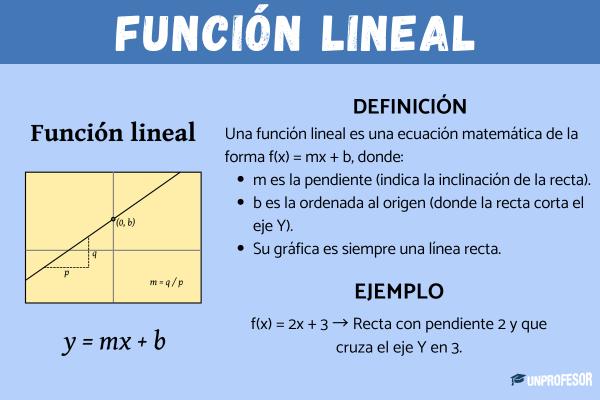
Para que acabes de entender qué es una función lineal, aquí te dejamos una lista con sus elementos principales:

• Variable o incógnita: esta variable representada por la letra x puede ser cualquier valor sin importar cuales sean los demás valores.
• Variable dependiente: es el valor que se obtiene cuando se intercambia el valor de x por un número, es decir su resultado denotado por y o f(x).
• Pendiente: la pendiente m determina cuál será la inclinación de la recta en la gráfica.
• Ordenada al origen: la ordenada b, es el corte que tendrá la recta en la gráfica con el eje.

Como mencionamos anteriormente, la pendiente determina la inclinación de la recta, entonces:

• Pendiente positiva: si la pendiente de la función lineal es positiva, es decir m>0, entonces la función será “creciente”.
• Pendiente negativa: si la pendiente de la función lineal es negativa, es decir m<0, entonces la función será “decreciente”

Rectas paralelas o perpendiculares

• Dos rectas de una función lineal son paralelas cuando sus pendientes son iguales, es decir cuando m de una función lineal es igual a m de la otra función lineal. Por ejemplo: 2 x + 3 es paralela a 2 x - 8, ya que m = 2 en ambas funciones lineales.
• Dos rectas de una función lineal son perpendiculares si sus pendientes son inversas y recíprocas, es decir si una pendiente es m y la otra es -1/m. Por ejemplo: 3 x + 4 es perpendicular a -1/3 x - 7 ya que m = 3 y m = -1/3.

Para graficar una función lineal debemos tener en cuenta que necesitamos dos puntos cualesquiera para hacerlo, ya que es una recta y por lo tanto con dos puntos podemos trazarla.

Para ellos, debemos encontrar dos puntos que pertenezcan a esa función lineal, es decir que son dos puntos que se escriben como: (x, f(x)) o (x,y).

Para ello, utilizamos una tabla, en donde asignamos valores a x, y reemplazamos ese valor en la función lineal que necesitamos graficar, y obtenemos como resultado y o f(x).

Luego, cuando encontramos los puntos necesarios, los ubicamos en el eje cartesiano y unimos con una recta, que será la recta de la función lineal.

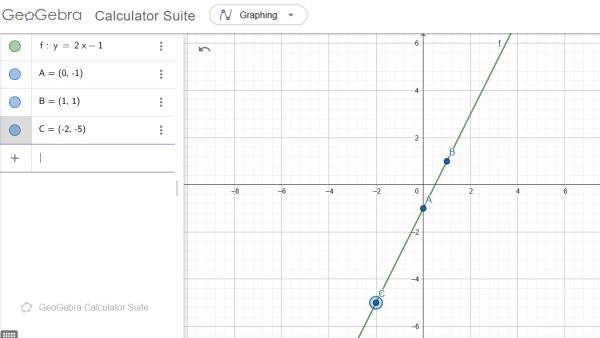
Ejemplo: f(x) = 2x - 1

En este caso, la pendiente es m = 2 y la ordenada al origen es b = -1. Ahora armamos la tabla para hallar varios puntos en el eje y trazar la recta. Los números elegidos como x, son aleatorios, pueden elegir cualquier número.

• xy
• 02 . 0 - 1 = -1
• 12 . 1 - 1 = 1
• -22 . (-2) - 1 = -5

Una vez que realizamos la tabla, escribimos cuáles son los pares de números que vamos a utilizar para trazar la recta, y en este caso son (0,-1), (1,1) y (-2, -5).

Los puntos de corte de una función lineal son aquellos puntos en los que la recta corta al eje x y al eje y. Esto puede calcularse reemplazando los valores de x e y por cero para hallarlos.

El corte con el eje x se encuentra reemplazando a y por cero, es decir, el resultado de la función debe dar cero, y se debe hallar qué valor de x cumple con esto. Entonces el punto se representa como: (x, 0).

En el ejemplo anterior, el punto de corte con el eje x sería:

• f(x) = 2 . x - 1 = 0
• 2 . x = 1
• x = 1/2
• Por lo tanto, la gráfica de la función lineal f(x) = 2x - 1 corta al eje x en (1/2, 0).

El corte con el eje y se encuentra reemplazando a x por cero, es decir que debemos encontrar para qué valor de y la x es igual a cero. Entonces el punto se representa como: (0, f(x)) o (0,y).

En el ejemplo anterior, el punto con el eje y sería:

f(0) = 2 . 0 - 1 = -1

Por lo tanto, la gráfica de la función lineal f(x) = 2x - 1 corta al eje y en (0,-1).

Podemos encontrar la ecuación de una función lineal a partir de dos puntos conocidos que pertenecen a la recta de esta. Para ello, debemos plantear un sistema de ecuaciones donde intercambiamos o reemplazamos los valores de los puntos (x,y) en las ecuaciones de una función lineal, para hallar así, la pendiente y la ordenada al origen.

Ejemplo

Veamos un ejemplo: Tenemos dos puntos pertenecientes a una función lineal, y queremos hallar la ecuación de la recta, sabiendo que pasa por (1,1) y (-3,5).

Utilizamos la ecuación de la función lineal general,

• y = mx + b

Reemplazamos los puntos en dos ecuaciones diferentes

• 1 = m . 1 + b
• 5 = m . (-3) + b

Ahora planteamos el sistema de ecuaciones, despejando b de la primera ecuación y reemplazando en la segunda.

b = 1 - m . 1

Entonces:

• 5 = m . (-3) + 1 - m . 1
• 5 = -3.m + 1 - 1.m
• 5 - 1 = -4.m
• 4 = -4.m
• -1 = m

Una vez que hallamos el valor de m, debemos encontrar el valor de b, y esto lo hacemos reemplazando el valor que encontramos en las dos ecuaciones para corroborar el resultado en ambas funciones.

Primera ecuación

• 1 = -1 . 1 + b
• 1 = -1 + b
• 1 + 1 = b
• 2 = b

Segunda ecuación

• 5 = -1 . (-3) + b
• 5 = 3 + b
• 5 - 3 = b
• 2 = b

Por lo tanto, m = -1 y b = 2 y la función lineal entonces es:

• y = -1 . x + 2

Si deseas leer más artículos parecidos a Qué es una función lineal: ejemplos, te recomendamos que entres en nuestra categoría de Álgebra.