División de fracciones


¡Descubre cómo hacer una buena división de fracciones! En unProfesor te dejamos esta lección completa donde encontrarás una explicación sencilla, junto con un vídeo de nuestra profesora de matemáticas. Además, te dejamos ejemplos de división de fracciones y ejercicios resueltos para que puedas practicar en casa. ¡Aprende matemáticas de forma más fácil gracias a nuestras lecciones online!
¿Cómo se hace la división de fracciones?
Para dividir fracciones lo primero que debemos recordar es que una fracción es el cociente entre dos números enteros. Es decir, una fracción es una división ya en sí misma. Sabiendo que la división es la operación inversa de la multiplicación, podemos utilizar este concepto para poder realizar la división entre fracciones.
Elementos de una división de fracciones
En toda división existe un dividendo, un divisor, un signo o símbolo y un resultado. El dividendo es aquel número que queremos dividir, mientras que el divisor será el número por el cual dividiremos al dividendo. El signo o símbolo en este caso es de división y se puede utilizar tanto : como /. Y por último el resultado o también llamado cociente que es el número final de la división.
Por ejemplo: 10/4 : 20/8 = 1/1. En este ejemplo el dividendo es 10/4, el divisor 20/8 y el resultado 1/1 o 1 entero.
Para dividir dos fracciones debemos multiplicar el dividendo por la fracción inversa del divisor. Dicho con otras palabras, la fracción que necesitamos dividir la multiplicaremos por la fracción inversa por la cual dividimos. Es decir,
a/b : c/d = a/b . d/c
Así mismo, cuando convertimos una división en una multiplicación podemos recordar que se puede simplificar tanto una fracción, entre numerador y denominador o de forma cruzada entre las dos fracciones que ahora se están multiplicando. Cuando simplificamos, nos referimos a encontrar un número que sea divisor de ambos y entonces “simplificarlo” es decir, hacerlo más pequeño para que la cuenta sea más sencilla.

Ejemplo de división de fracciones
Queremos dividir las siguientes fracciones y encontrar su resultado. Entonces:
7/6 : 28/36 =
Primer paso a seguir, debemos convertir la división en multiplicación invirtiendo el divisor, en este caso 28/36.
7/6 . 36/28 =
Como 7 y 28 son multiplos, ambos pueden dividirse por 7, entonces simplificamos esos dos números de forma cruzada, el 7/7 = 1 y 28/7 = 4. Así mismo, como el 6 y 36 son múltiplos pueden dividirse por 6 y simplificarse de forma cruzada, entonces 6/6=1 y 36/6=6. Por lo tanto las fracciones simplificadas quedarían:
7/6 : 28/36 = 7/6 . 36/28 = 1/1 . 6/4 =
Ahora realizamos la multiplicación, donde se realiza el producto del numerador con el numerador y denominador con denominador.
7/6 : 28/36 = 7/6 . 36/28 = 1/1 . 6/4 = 6/4
La fracción que obtenemos al final, podemos simplificar ya que ambos números son divisibles por 2, entonces el cociente quedaría igual a:
7/6 : 28/36 = 7/6 . 36/28 = 1/1 . 6/4 = 6/4 = 3/2
En el caso en que la división sea entre una fracción y un número entero, a este último se le agrega un 1 como denominador y por lo tanto conseguimos una división entre dos fracciones, sin cambiar el resultado.
Descubre aquí los diferentes tipos de fracciones.
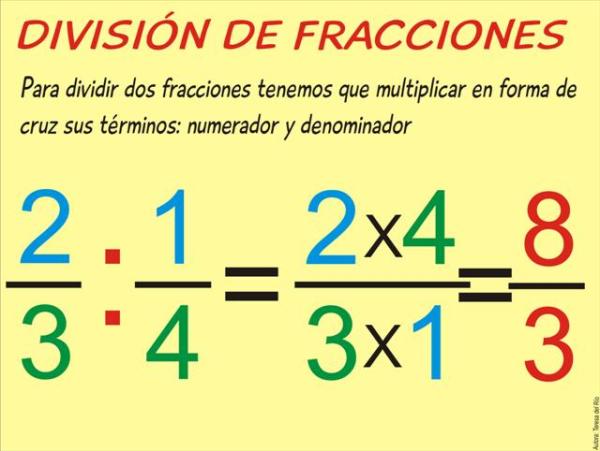
¿Cómo dividir fracciones en su forma más simple? Ejemplo
Se puede dividir de forma simple las fracciones, sin realizar todo el proceso que vimos anteriormente, pero no tiene la ventaja de simplificar previamente al resultado, por lo que si las fracciones son números muy elevados, deberemos primero multiplicar esos números grandes, y luego simplificar el resultado.
El segundo método es realizar el producto cruzado del numerador del dividendo con el denominador del divisor, siendo el resultado de esta operación el numerador del cociente. Y el producto cruzado del denominador del dividendo con el numerador del divisor, siendo el resultado de esta operación el denominador del cociente. Es decir:
a/b : c/d = (a.d) : (b.c)
Ejemplo
Queremos dividir las siguientes fracciones:
5/7 : 2/3 =
Primer paso, ubicamos los extremos, entonces multiplicamos cruzado, 5.3 y 7.2
5/7 : 2/3 = (5.3) / (7.2) = 15/14
En este caso, los números son pequeños y no pueden simplificarse, en el caso en que sea posible, simplificar el resultado.

¿Cómo se dividen fracciones con el mismo denominador?
Las fracciones que poseen el mismo denominador son las más simples de resolver, ya que teniendo en cuenta el primer método podremos simplificar fácilmente el denominador y así obtener como resultado una fracción que se compone del numerador del dividendo y el denominador del divisor.
Ejemplo
Veamos un ejemplo.
Queremos dividir las siguientes fracciones con el mismo denominador:
12/5 : 36/5 =
Primero, invertimos la fracción del divisor, pasamos la división a multiplicación y simplificamos cruzado. Como los denominadores son iguales, al aplicar la simplificación cruzada, podremos siempre dividir por ese número, y entonces obtener 1 en cada uno de ellos, es decir:
12/5 : 36/5 = 12/5 . 5/36 = 12/1 . 1/36 =
Así mismo, puede simplificar el 12 y 36 por 12, ya que ambos son divisibles por 12, y obtenemos:
12/5 : 36/5 = 12/5 . 5/36 = 12/1 . 1/36 = 1/1 . 1/3 = 1/3
El resultado es 1/3 .
Aquí te dejamos una comparación de fracciones con distinto denominador.

División de fracciones con distinto denominador: ejercicios resueltos
Realizamos los siguientes ejercicios de división de fracciones con diferente denominador de las dos formas aprendidas.
1- 7/3 : 4/5 =
2- 15/18 : 25/9 =
3- 40/7 : 8/42 =
4- 2/7 : 4 =
Soluciones
1- Utilizamos el segundo método, es decir la forma sencilla para resolver 7/3 : 4/5 =
Multiplicamos 7.5 y 3.4 entonces:
7/3 : 4/5 = (7.5) / (3.4) = 35/12
2- Utilizamos el primer método para resolver 15/18 : 25/9 =
15/18 : 25/9 = 15/18 . 9/25 =
Simplificamos,
15/18 : 25/9 = 15/18 . 9/25 = 3/2 . 1/5 = 3/10
3- Utilizamos el primer método para resolver 40/7 : 8/42 =
40/7 : 8/42 = 40/7 . 42/8 =
Simplificamos,
40/7 : 8/42 = 40/7 . 42/8 = 5/1 . 6/1 = 30/1 = 30
4- Utilizamos el primer método para resolver 2/7 : 4 =
Agregamos un 1 como denominador del entero 4, para convertirlo así en fracción sin modificar el valor.
2/7 : 4 = 2/7 : 4/1 = 2/7 . 1/4 =
Simplificamos,
2/7 : 4 = 2/7 : 4/1 = 2/7 . 1/4 = 1/7 . 1/2 = 1/14
Si deseas leer más artículos parecidos a División de fracciones, te recomendamos que entres en nuestra categoría de Aritmética.












