Cuáles son los elementos de un ángulo

Un ángulo es la apertura entre dos semirrectas que poseen un origen en común. Las semirrectas que lo componen se denominan lados y el punto de origen se llama vértice. El ángulo vendría a ser la porción de plano que está entre las semirrectas. Los ángulos pueden medirse en grados sexagesimales o en radianes.

Ahora bien, los elementos de un ángulo son justamente los que nombramos anteriormente, es decir que forman parte de su definición. Por lo tanto, los elementos de un ángulo son:

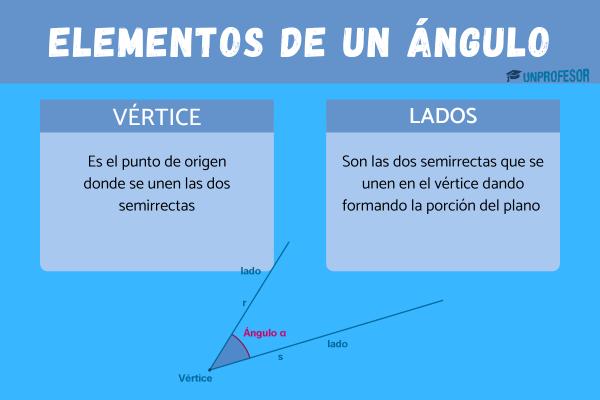
• Vértice: es el punto de origen donde se unen las dos semirrectas
• Lados: son las dos semirrectas que se unen en el vértice dando formando la porción del plano

Estos elementos que componen los ángulos son siempre los mismos, es decir que si o si debemos tener un vértice que une dos semirrectas formando una apertura, y por lo tanto un ángulo.

Existen diferentes tipos de ángulos, y pueden clasificarse de acuerdo a diferentes criterios como por ejemplo, según su amplitud o según la relación que tenga con otro ángulo. Pero debemos tener en cuenta que los elementos que forman a cualquier ángulo siempre son dos lados y un vértice.

Un ángulo recto se forma por la unión de dos líneas rectas que se cruzan formando una esquina perfecta.

Las dos líneas como los lados de esa esquina. El punto donde se juntan esas dos líneas se llama vértice del ángulo.

La característica principal de un ángulo recto es que mide exactamente 90 grados (90º). Este tipo de ángulo se puede ver en ejemplos reales como, por ejemplo, la esquina de un libro, una mesa o una pared.

Así pues, los elementos que forman un ángulo recto son:

• Dos líneas rectas (o segmentos de recta).
• Un punto donde se unen estas líneas (vértice).
• Una abertura entre las líneas que mide 90 grados.

Como mencionamos anteriormente, los ángulos pueden clasificarse según diferentes criterios. Veamos cuáles son.

Según la amplitud del ángulo

• Ángulo nulo: un ángulo nulo es aquel que mide 0° sexagesimales, es decir su amplitud es cero.
• Ángulo agudo: un ángulo agudo es aquel que mide más de 0° sexagesimales pero menos que 90° sexagesimales.
• Ángulo recto: un ángulo recto es aquel que mide exactamente 90° sexagesimales.
• Ángulo obtuso: un ángulo obtuso es aquel que mide más de 90° sexagesimales pero menos que 180° sexagesimales.
• Ángulo llano: un ángulo llano es aquel que mide exactamente 180° sexagesimales.
• Ángulo cóncavo: un ángulo cóncavo mide más que 180° sexagesimales.
• Ángulo completo: un ángulo completo mide exactamente 360° sexagesimales. Es el ángulo que completa la vuelta.

Según la relación que posee con otro ángulo

• Ángulos complementarios: los ángulos complementarios son dos ángulos que están unidos por el vértice y que comparten uno de sus lados, sumando entre los dos 90° sexagesimales. Es decir, son dos ángulos cuya suma arroja como resultado un ángulo recto.
• Ángulos suplementarios: los ángulos suplementarios son dos ángulos que están unidos por el vértice y que comparten uno de sus lados, sumando entre los dos 180° sexagesimales. Es decir, son dos ángulos cuya suma arroja como resultado un ángulo llano.

Según la posición de los ángulos

• Ángulos opuestos por el vértice: los ángulos opuestos por el vértice son justamente ángulos que comparten el vértice pero ninguno de sus lados.
• Ángulos consecutivos: los ángulos consecutivos son aquellos que comparten uno de sus lados y el vértice.
• Ángulos adyacentes: los ángulos adyacentes son aquellos que son ángulos consecutivos y a su vez el lado que no comparten se encuentra en la misma recta.

Para poder medir la amplitud que tenemos en un ángulo, debemos utilizar un instrumento para ello. En este caso, se utiliza un transportador o semicírculo que se encuentra graduado en grados para medirlo. Suelen tener forma circular o semicircular y son generalmente de plástico.

Para poder medir la amplitud se deben seguir los siguientes pasos:

1. Debemos colocar el punto cero, es decir el centro del transportador en el vértice del ángulo que necesitamos medir. Es decir, el centro del instrumento con el punto de origen del ángulo.
2. Debemos tener en cuenta que uno de los lados del ángulo, debe coincidir con el ángulo cero del transportador, es decir con la base del mismo para realizar la medición correctamente.
3. Ubicamos el número en grados en el cual el lado restante será coincidente, y de esta manera encontramos el valor de la amplitud.

Los ángulos interiores son muy utilizados en matemáticas, y sobre todo en la geometría. A partir de ellos, podemos clasificar también a los polígonos.

Por ejemplo, sabemos que un triángulo está formado por tres lados, tres vértices y tres ángulos interiores. A partir de estos ángulos interiores existe una clasificación para los triángulos, es decir:

• Si un triángulo posee uno de sus ángulos rectos, entonces el triángulo se denomina triángulo rectángulo.
• Mientras que si un triángulo tiene uno de sus lados interiores obtuso, el triángulo será llamado triángulo obtusángulo.
• Si por el contrario tiene tres ángulos agudos, se denominará triángulo acutángulo.

Este es uno de los ejemplos que podemos encontrar en los polígonos, pero recordemos que los cuadrados y rectángulos, son figuras que están formadas por cuatro ángulos y estos son todos rectos. El rombo tiene cuatro ángulos también, pero tiene dos pares de ángulos iguales. Todas estas particularidades con los ángulos que poseen estas figuras geométricas, son importantes a la hora de realizar cálculos y reconocerlos por sus características.

Además de esto, los ángulos interiores se utilizan también por ejemplo, para las razones trigonométricas. Ya que dependiendo del ángulo del triángulo que utilizamos, podemos usar el coseno, el seno o la tangente para calcular un valor faltante.

Los ángulos interiores, por lo tanto, son muy importantes a la hora de realizar cálculos, conjeturas, y hasta ejercicios complejos.

Si deseas leer más artículos parecidos a Cuáles son los elementos de un ángulo, te recomendamos que entres en nuestra categoría de Geometría.